УДК 621.396.61
Разработка моделей функциональных узлов выходной ступени тракта передачи (продолжение)
4.5 Разработка модели источника испытательного двухчастотного сигнала
Линейность тракта передачи принято оценивать двухчастотным методом [1]. В соответствии с этим методом на вход транзистора подаются два сигнала одинаковой амплитуды с близкими частотами ω1 и ω2 (рисунок 4.13), а на выходе определяется отношение амплитуд комбинационных составляющих третьего и пятого порядков (сигналов с частотами 2ω1 — ω2, 2ω2 — ω1, 3ω1 — 2ω2, 3ω2 — 2ω1) к амплитуде основных сигналов ( рисунок 4.14). Для идеальной линейной системы комбинационные составляющие равны нулю.
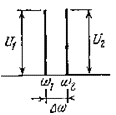
Рисунок 4.13 - Спектр сигнала на входе усилителя.
Принцип измерения уровня нелинейных комбинационных искажений третьего порядка M3 состоит в том, что после достижения требуемого уровня мощности Рвых измеряется отношение наибольшей из двух амплитуд комбинационных частот 2ω1 — ω2 и ω2 — ω1 к амплитуде основных тонов U (рисунок 4.14). 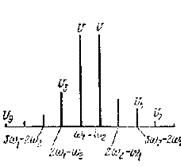
Рисунок 4.14 - Часть спектра сигнала в нагрузке.
Выражение для определения М3 (в децибелах) имеет вид [1]:
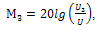 (4.4), а для М5 (4.4), а для М5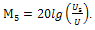 (4.5) (4.5)
Таким образом, модель испытательного двухчастотного сигнала должна состоять из двух источников высокочастотного сигнала с частотами, отличающимися друг от друга ~0,1%, и сумматора. Схема модели приведена на рисунке 4.15.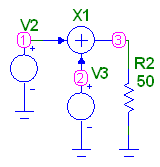
Рисунок 4.15 – Схема модели источника испытательного двухчастотного сигнала.
На схеме V2(t) и V3(t) – источники высокочастотного сигнала.
Х1 – идеальный сумматор [2], обеспечивающий суммирование сигналов V2 и V3 по формуле:
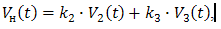 (4.6) (4.6)
где: V2 – первый высокочастотный сигнал в узле 1;
- V3 - второй высокочастотный сигнал в узле 2 с частотой большей или меньшей частоты первого высокочастотного сигнала на ~ 0.1% от установленного значения частоты первого генератора;
k2 и k3 – коэффициенты пропорциональности по первому и второму входу сумматора. На рисунке 4.16 приведены эпюры входных и выходного сигналов модели.
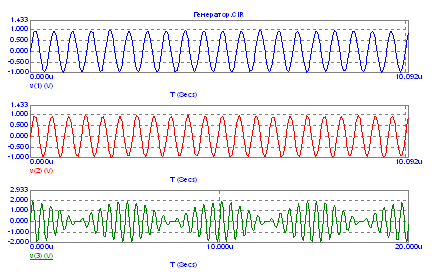
Рисунок 4.16 – Эпюры входных и выходного сигналов
4.6 Разработка модели фильтра гармоник и исследование его работы при комплексной нагрузке выхода
Основной задачей моделирования является исследование мощного выходного каскада тракта передачи в условиях подключения к выходу его фильтров гармоник комплексной нагрузки с заданным значением КСВ.
Данный режим работы возникает при подключении выхода передатчика к широкополосной антенне, широкополосным согласующим устройствам, или при работе в режиме ППРЧ, известном в зарубежной литературе как режим FH [3].
Идентичность построения отдельных каналов фильтра гармоник (см. рисунок 4.2 предыдущей статьи) позволяет для моделирования его поведения в условиях рассогласования по выходу провести исследование одного из его каналов.
Для анализа выбираем фильтр диапазона частот от 2 до 2,94 МГц. Схема выбранного канала фильтра для проведения его моделирования изображена на рисунке 4.17.
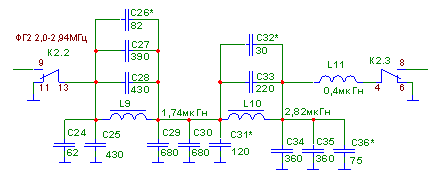
Рисунок 4.17 – Схема фильтра гармоник на частоты от 2 до 2,94 МГц
Схема модели фильтра диапазона от 2 до 2,94 МГц приведена на рисунке 4.18.
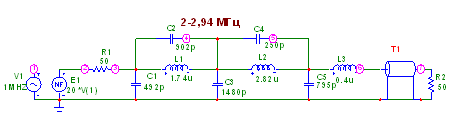
Рисунок 4.18 – Схема модели фильтра диапазона 2-2,94 МГц
На рисунке 4.18 источником сигнала является зависимый генератор Е1 с внутренним сопротивлением R1, равным 50 Ом. Зависимый генератор управляется от стандартного идеального источника V1, диапазон изменения, частоты которого задается режимом моделирования схемы [2]. Коэффициент пропорциональности определяется уровнем входной мощности фильтра. В нашем случае коэффициент пропорциональности равный 20 определяет уровень входной мощности 8 Вт.
Длинная линия Т1 обеспечивает формирование комплексного сопротивления нагрузки фильтра, определяемого ее входным сопротивлением, которое в свою очередь зависит от сопротивления нагрузки R2 выхода длинной линии Т1 . Значение сопротивления нагрузки линии Т1 определяет круг КСВ, в пределах которого будет изменяться входное сопротивление фильтра.
Волновое сопротивление линии Т1 выбираем равным оптимальному сопротивлению нагрузки фильтра гармоник 50 Ом.
Имитация работы фильтра на комплексную нагрузку с заданным КСВ обеспечивается изменением номинального значения сопротивления нагрузки R2 линии Т1. Для формирования входного комплексного сопротивления в круге КСВ=2 сопротивление R2 должно быть равным 100 или 25 Ом.
На рисунке 4.18 изображена схема модели, соответствующая режиму согласованной нагрузки для фильтра гармоник с номинальным сопротивлением нагрузки 50 Ом.
Результаты моделирования фильтра в согласованном режиме приведены на рисунке 4.19, 4.20.
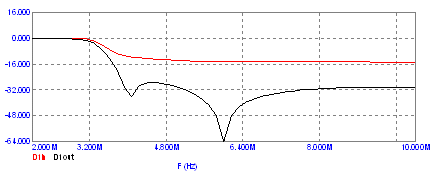
Рисунок 4.19 – Амплитудно-частотные характеристики
фильтра в согласованном режиме.
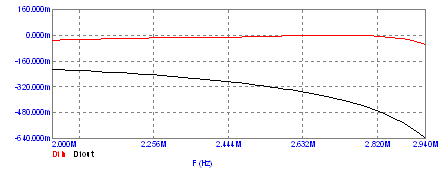 Рисунок 4.20 – Амплитудно-частотная характеристика потерь фильтра в полосе пропускания.
Из рисунка 4.19 следует, что в согласованном режиме фильтр обеспечивает подавление гармонических составляющих не менее чем на 28 дБ при выбранных добротностях индуктивных и емкостных элементов 100.
Потери в полосе пропускания фильтра не превышают минус 0,64 дБ.
Характер изменения коэффициента отражения на входе фильтра Готр вх от коэффициента отражения на его выходе Готр вых в виде круговой диаграммы Вольперта - Смитта в рабочей полосе частот показан на рисунке 4.21.
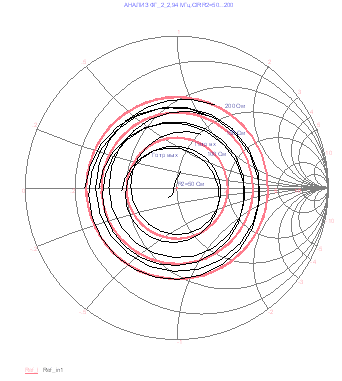
Рисунок 4.21 – Частотная характеристика коэффициентов отражения на входе и выходе фильтра.
Изменение коэффициента отражения на выходе фильтра обеспечивается изменением сопротивления нагрузки R2 длинной линии Т1 с установленным шагом, равным 50 Ом.
Из рисунка видно, что рассогласование на выходе фильтра трансформируется к его входу, оставаясь в круге КСВ, заданном нагрузкой длинной линии и не превышает установленного ей значения.
Отсюда следует вывод, что рассогласование на выходе фильтра гармоник не приводит к увеличению значения КСВ, подводимого к выходу усилителя мощности выходной ступени РПДУ.
Графики зависимости потерь в фильтре в полосе его пропускания от значения КСВ на его выходе и частоты приведены на рисунке 4.22.
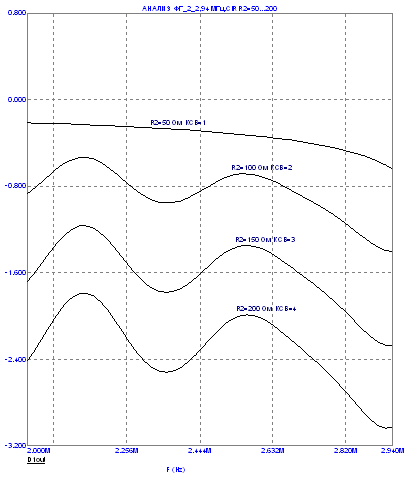
Рисунок 4.22 – Графики зависимости потерь в фильтре от значения КСВ на его выходе и частоты.
На рисунке 4.23 приведены границы области потерь рассогласования в фильтре в зависимости от значения КСВ его нагрузки.
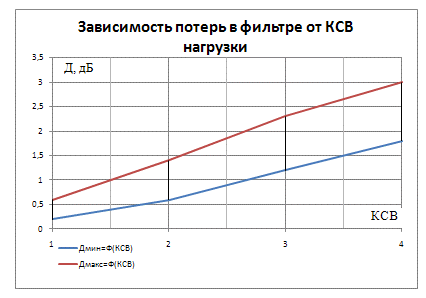
Рисунок 4.23 – Границы области потерь рассогласования в фильтре в зависимости от КСВ нагрузки.
Из рисунка 4.23 видно, что потери из-за рассогласования по выходу фильтра увеличиваются практически линейно от 0,6 дБ (в режиме согласования КСВ=1) до 3 дБ при КСВ=4 и могут быть представлены аппроксимирующей функцией вида:
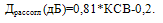 (4.7) (4.7)
Характеристика фильтра в диапазоне до 10 МГц и режиме рассогласования ( при изменении нагрузки от 50 Ом до 200 Ом с шагом 50 Ом) представлена на рисунке 4.24.
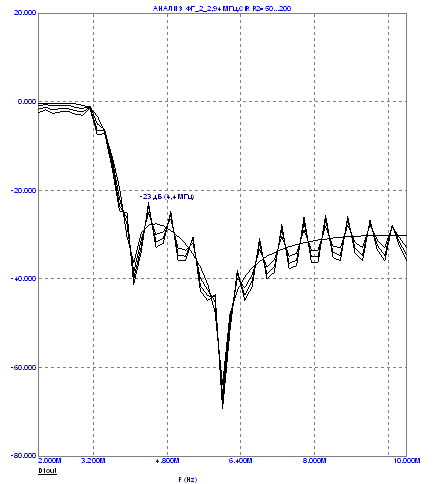
Рисунок 4.24 – Характеристика фильтра в режиме рассогласования по выходу.
Из рисунков 4.19, 4.20 и 4.24 следует, что режим рассогласования на выходе фильтра незначительно отражается на его фильтрующей способности – в наихудшей точке на частоте 4,4 МГц подавление уменьшается с минус 28 дБ в согласованном режиме до минус 23 дБ в режиме максимального рассогласования.
Выводы
В статье описана модель источника испытательного двухчастотного сигнала и проведено исследование поведения фильтра гармоник при его работе на комплексную нагрузку.
Определена аппроксимирующая функция потерь в фильтре гармоник и оценено изменение его фильтрующих свойств в в режиме работы на КСВ от 1 до 4.
СПИСОК ЛИТЕРАТУРЫ
- Ю.В. Завражнов, И.И. Каганов, Е.З. Мазель, А.И. Миркин. Мощные высокочастотные транзисторы/ Под ред. Е.З. Мазеля. –М.: Радио и связь, 1985. 176с.
- Micro-CAP 9. Electronic Circuit Analysis Program Reference Manual. Spectrum Software, 2007.
- Бернард Скляр. Цифровая связь. Теоретически основы и практическое применение. Второе издание, исправленное. – Москва-Санкт-Петербург-Киев, издательский дом «Вильямс», 2003, 1104 с.
| 




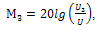 (4.4), а для М5
(4.4), а для М5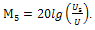 (4.5)
(4.5)
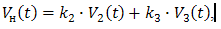 (4.6)
(4.6)







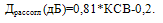 (4.7)
(4.7)